
数学家们证伪了“望远镜猜想”。关于用稳定同伦群探索高维孔洞,数学家认为,“我们不仅证明了这种方法行不通,更证明了这种方法失败地非常彻底。这座宅邸比我们预想的要复杂太多。”
撰文 | Marianne Freiberger
翻译 | wnkwef
审校 | 悦悦
在拓扑学领域中出现了一个令人振奋的突破:一群数学家证伪了“望远镜猜想”。这一猜想由道格拉斯·拉维尼尔在1984年提出,因作为他一系列猜想中最后被解决的一个而闻名。
这一研究团队在剑桥艾萨克·牛顿数学科学研究所(INI)组织的“同伦理论全景”会议上宣布了他们的研究成果,托默·施兰克(Tomer Schlank)、杰里米·哈恩(Jeremy Hahn)、罗伯特·伯克伦德(Robert Burklund)和伊山·利维(Ishan Levy)共同完成了这一结果的证明。我们邀请到了托默·施兰克和杰里米·哈恩,用尽可能最简单的语言来介绍他们的工作。以下是他们告诉我们的内容。
什么是拓扑学?
对于几何形状,拓扑学采取的态度和我们在日常生活中一样宽松。当我们说高尔夫球是球形的时候,我们并不关心它上面有许多小凹点,严格来说,这就意味着它并不是一个完美的球面。同样,尽管橘子和苹果明显凹凸不平,我们也会认为它们是圆的。
拓扑学体现出了这种对于变形的容忍度。如果两个形状能够通过挤压或者拉伸(而非切割或粘合)相互转换,那么它们在拓扑学上就会被认为是相同的。从这个意义上讲,高尔夫球、橘子、苹果和漏气的足球都是一样的。类似地,甜甜圈在拓扑学上与咖啡杯相同(如下面的gif动图所示)。不过,甜甜圈和球面并不相同,因为将球面变成甜甜圈的唯一方法只能是在球面上切出一个洞,再把边缘粘合起来。
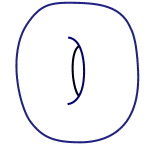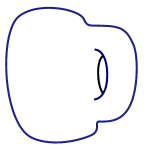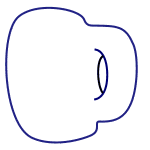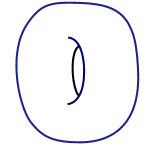
一个马克杯先变成甜甜圈,再变回马克杯的样子。
甜甜圈(严格来说是圆环面)和球面的区别在于,圆环面有一个洞,而球面没有。事实上,洞在拓扑学中是极其重要的。数学家已经证明了许多自然而然地出现在我们脑海中的表面结构在拓扑学上都等价于球面(即没有任何洞)、圆环面(有一个洞),又或者是具有两个、三个洞等的圆环面。在拓扑学中,我们使用洞的数量定义表面。

球面,圆环面,具有有两个洞和三个洞的表面。
走一条环路
现在也许你会问“什么是洞?”在看到一个圆环面时,我们很清楚它确实有一个洞。但一旦你试图将“有洞”的属性用语言描述出来时,事情就会变得有些棘手。
这时,我们可以利用圆圈来帮忙。你在拓扑球上可能画出的任何圆圈都能够收缩成一个点。而对于拓扑圆环面,或者其他有洞的表面,情况会有些出入:如果圆圈绕着洞旋转,你可以尽情地推动或者挪动它,但是只要你不把表面粘合在一起,它永远也不会收缩成一个点。
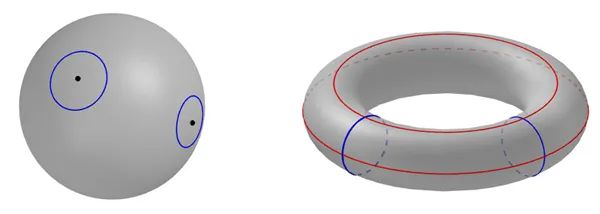
左图中球面上的圆圈都可以缩小成一个点,例如收缩到它们的中心点。右图中蓝色和红色的圆圈不能收缩成一个点,因为它们在围绕着洞旋转。颜色相同的圆圈在不进行切割或粘合的操作下能够互相转换。它们彼此之间同伦等价。在球面上,所有的圆圈都同伦等价于一个半径为0的最简单的圆,即一个点。然而,在圆环面上,依据圆圈围绕洞旋转的方式,可以定义不同类型的圆。
如果你的拓扑球是一颗高尔夫球,或者你的拓扑圆环面是一个弯曲的甜甜圈,那么受凹陷和凸起影响,你不可能在任何一个面上画出一个完美的圆。但我们不必担心这一点,我们追求的是一般性的圆,也就是闭合的环路。
我们同样不用区分那些不进行切割,而通过比如在表面上滑动、拉伸或是挤压的方式就可以相互转换的环路。这些环路可以被认为是等价的,我们可以将在曲面上绘制的环路的集合划分为等价类。如果两条环路可以在不进行切割的情况下相互转换,它们便属于同一个类,在上面的图片中,颜色相同的环路属于同一个等价类。
以上所有这些都可以在数学上精确地表述出来:表面上的环路的等价类被称为同伦类,所有这些等价类的集合被称为表面的同伦群。同伦群的确切构成提供了关于表面的洞的信息,因此能够告诉我们很多关于表面本身的信息(是的,它构成了数学上的一个群)。
二维孔洞
一旦你认识到孔洞对于描述表面的重要性,以及环路对于描述孔洞的重要性,你可能会问自己如何才能继续进行下去。
到目前为止,我们已经考虑了能够绘制在表面上的环路,换句话说,也就是能够在表面上连续地映射一个圆的所有可能方式。“映射”圆仅仅意味着将圆上的每一个点分配给表面上的一个点,而“连续”意味着在得到的环路中没有间隙。
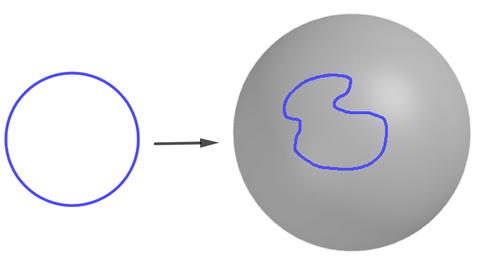
在球面上展示的蓝色环路是由圆变形得到的。严格地讲,它是从圆到球面进行连续映射得到的图像。
圆是球面的一维类比。如果我们再提高一个维度,还会有什么方式可以将球连续映射到我们的表面呢?如果表面本身就是一个拓扑球,比如说一个漏气的足球,那么很容易就能想象出实现这一映射的方法。你可以将球面变形,直到它具有和足球完全相同的形状,然后再将变形之后的球面上的每一个点分配给足球上对应的点。

想到一种将球面连续映射到漏气的足球的方式是很容易的。
你也可以很容易地将球面映射到包含有拓扑球的形状上,如下图所示。
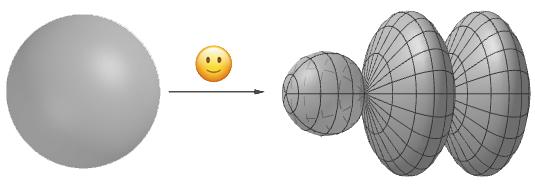
可以将球面连续映射到右图中左侧的球状部分上。
不过,你会发现不能将球面映射到拓扑圆环面,孔洞再一次变成了难题。
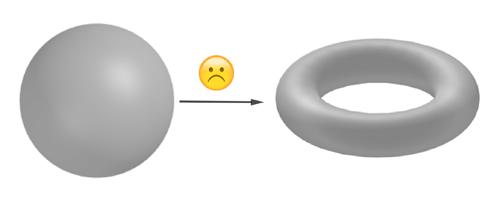
很难想到一种将球面映射到圆环面的方式,除非将球面进行切割,或将它压扁为一个二维薄片,再想象着把它粘贴在圆环面上。这样一个薄片同伦等价于一个点。因此,考虑同伦的情况下,将球面连续映射到圆环面的唯一方式是平凡的,它将整个球面映射到一个单独的点上。
在前两个例子中,一旦球面被映射到一个表面上,就不再可能在表面本身不形变的情况下将球面缩小到一个点。这是因为它包围了你所认为的二维孔洞,也就是你想要映射到的拓扑球的内部。
“球面没有任何一维孔洞,因为每当你画一条环路的时候,你都可以将它缩小,”托默·施兰克说。“但球面确实有一个二维孔洞,因为你可以映射另一个球面到它上面,使它不能被缩小。这虽然不直观,但不难证明:圆环面不存在二维孔洞。”
这些想法可以用数学语言精确地表达出来。与我们之前看到的关于环路的情况类似,你最终可以得到一个曲面的同伦群,它可以告诉你二维孔洞的存在。一般来说,这一同伦群由将球面连续映射到其他表面的所有方法生成,可以用于判断被映射的表面能否收缩到一点。
高维孔洞和形状
现在,我们知道,圆是一维的客体,而球面是一个平面,即二维的。尽管我们不能直观地看到高维表面,数学家们却有定义它们的方法。因此你可以像处理圆或者普通的球面那样去处理它们。
类似地,现在你可以定义将高维球面映射到给定形状的同伦群。这些同伦群将会为你提供形状中那些你所认为的高维孔洞的信息。
“有些事情令人惊讶,并且在定义同伦群时也没有被预想到,那就是你可以在低维球面中得到高维孔洞,”施兰克解释道。“比如说,你可以写下一种从三维球面到二维球面的连续映射,并且不能收缩成一个点。”这意味着这种二维球面具有一个三维孔洞。尽管它超出了我们能够想象到的范围,但是下面的图像描绘了这种映射。你不需要去理解它——我们把它放在这里,只是想说数学家们确实对于他们所讨论的内容有着清晰的概念。

图像描绘了霍普夫纤维化(Hopf fibration),一种从三维球面到二维球面的非平凡映射。图:Niles Johnson,CC BY 4.0。
现在,我们可以考虑二维球面是否具有四维、五维、六维等更高维度的孔洞。更一般地,在给定球面的维度n后,可以考虑是否存在具有更高维度m的孔洞。对应的同伦群用πm(Sn)进行表示。下标m是要寻找的孔洞的维数,而上标n是洞所在的表面的维度。
“理解‘由球面之间的映射产生的同伦群是什么’这一一般性的问题,仍然是同伦理论领域中的关键课题,”施兰克说。换句话说,数学家们希望能够进一步理解遍历m和n所有组合方式的同伦群πm(Sn)。
事实证明,这在目前是一个不可能实现的任务,但好在数学的本质可以为我们提供有效的简化。数学家汉斯·弗赖登塔尔(Hans Freudenthal)在1937年证明,只要包含的维数差 (m-n) 相同并且n足够大,同伦群πm(Sn)便都是相同的(严格来讲它们彼此同构)。这表示存在着在整个分支上都彼此相同的同伦群。例如:
在这里,维数的差是1。
在这里,维数的差是2。
在这里,维数的差是3。
符号代表这些群在本质上是相同的(即彼此同构)。
在这些分支中的同伦群被称为稳定同伦群。对于每一个整数,都存在着一个稳定同伦群:它包含一个维数之差为1的同伦群,一个维数之差为2的同伦群,以此类推。“所以我们可以先来尝试一个比较简单的问题,只去研究这些稳定同伦群,而非所有的同伦群。”施兰克说。
戏剧性的失败
稳定同伦群能够使问题变得更加容易,但想要理解它并不轻松。道格拉斯·拉维尼尔在1984年提出了望远镜猜想。他曾表示,不会指望他的孙辈能够在有生之年完全理解其中的所有内容。这也是数学家们停止了对于个别稳定同伦群的关注,转而去尝试理解它们的整体结构的原因。拉维尼尔将这种行为比作身处一座巨大的宅邸之中。与其调查每一个房间,你更愿意去理解建筑整体的结构。

数学家汉斯·弗赖登塔尔对同伦理论做出了巨大的贡献。这幅肖像拍摄于1957年。图:Hofland, L.H., Het Utrechts Archief,CC BY 4.0。
望远镜猜想使得掌握同伦群整体的结构变为可能。但如今,伯克伦德、哈恩、利维和施兰克证明了这种猜想是错误的。这意味着拉维尼尔提供的方法行不通。“我认为公平地说,我们不仅证明了这种方法行不通,更证明了这种方法失败地非常彻底。这座宅邸比我们预想的要复杂太多。”哈恩说。
希望尚存
但这并不意味着我们回到了起点。我们对于稳定同伦群的了解表明,在它们的集合中存在着某种模式。你可以将这种模式按照类似于光的波长进行分解,每一个独立的波长都会展现出周期性的现象。“这些周期确实存在,但是远比望远镜猜想所预期的更加复杂,”施兰克说。“不过,我们证伪望远镜猜想的方式带给了我们一些有益的启发,”他补充道。“比如说,它为同伦群的大小提供了一个下限。”
伯克伦德、哈恩、利维和施兰克在牛津会议上宣布了他们的成果,并得到了巨大的赞誉。“这对我们所有人来说都是一个特别的时刻”,哈恩说到。“拉维尼尔在那里,迈克·霍普金斯也在。他与合作者一起证明了拉维尼尔的绝大多数猜想,除了望远镜猜想。会议室里聚集了与这些猜想有过交集的人们的整个历史。我们非常感激这次会议,它让所有这些人都聚集在一起。现在看起来是解释我们工作的最佳时机。”事实上,这次会议是为了致敬迈克·霍普金斯。这是一个由艾萨克·牛顿数学科学研究院(INI)举办的历时两周的活动的一部分。第二部分“同伦:沃土之果”在剑桥的INI举行。
历经近40年,在拉维尼尔提出的猜想全部解决之后,同伦理论领域开始迈向新的发展方向,以更好地理解稳定同伦群。INI在这一领域的探索中发挥了自己的作用:近期的会议是2018发起的一项研究计划的延续。或许在将来,它还会主持重要研究结果的发布。如果我们仍然在场,我们一定会报道这些信息。
本文经授权转载自微信公众号“中科院物理所”。
原文链接:Spheres within spheres:A journey through many dimensions. https://plus.maths.org/content/spheres-within-spheres-journey-through-many-dimensions
